Dam101_unitfour

Hyperparameter Tuning, Regularisation and Optimization

In this blog, we will run through how to tune the best hyperparameter settings and adjust the AI model’s internal parameters to minimize the prediction error. Regularisation

Regularisation

Regularization in deep learning refers to techniques used to prevent overfitting, ensuring that a model generalizes well to new, unseen data.

Correcte fit Vs over fit

If the model is able to perform well on the testing dataset, the model can be said to have generalized well, i.e., correctly understood the patterns provided in the training dataset. This type of model is called a correct fit model.

However, if the model performs really well on the training data and doesn’t perform well on the testing data, it can be concluded that the model has memorized the patterns of training data but is not able to generalize well on unseen data. This model is called an overfit model.

To summarize, overfitting is a phenomenon where the machine learning model learns patterns and performs well on data that it has been trained on and does not perform well on unseen data.

Methods used to handle overfitting of data.

• Training on more training data to better identify the patterns.
• Data augmentation for better model generalization.
• Regularization techniques.

In these techniques, data augmentation and more training data don’t change the model architecture but try to improve the performance by altering the input data.

Regularization is a technique used to address overfitting by directly changing the architecture of the model by modifying the model’s training process.

Commonly used regularization techniques are :

1. L2 regularization
2. L1 regularization
3. Dropout regularization.

Normalizing inputs

Normalization is a data preparation technique that is frequently used in machine learning. The process of transforming the columns in a dataset to the same scale is referred to as normalization.

Why normalization ?

Different scales of inputs cause different weight updates and optimizer steps; therefore, the values are all scaled between a certain range.

Example if we are handling image data then all the pixel value is divided by 255 and it is normalized in between 0 and 1.

Vanishing/ Exploding Gradients

Vanishing gradient and exploding gradient descent is a common problem that is faced while implementing deep neural networks.

Vanishing gradient descent

Vanishing gradient problem is a phenomenon that occurs during the training of deep neural networks, where the gradients that are used to update the network become extremely small or “vanish” as they are back propagated from the output layers to the earlier layers.

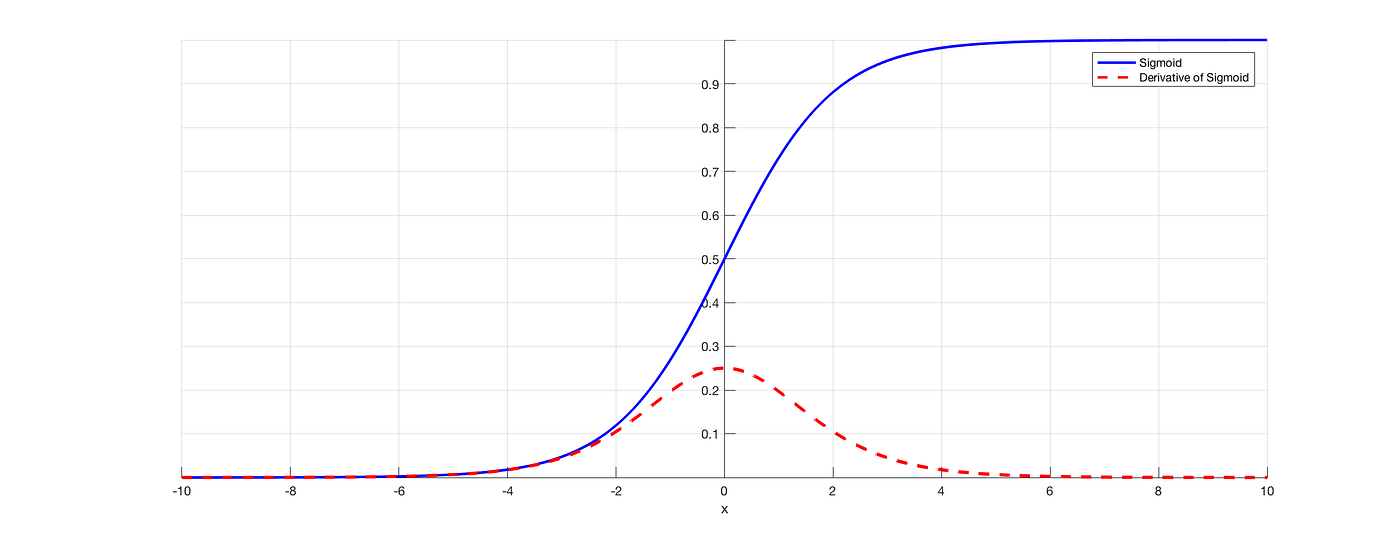
Vanishing gradient problem occurs due to sigmoid activation function.

During the training process of the neural network, the goal is to minimize a loss function by adjusting the weights of the network.

The vanishing gradient problem results in taking more time to converge to the global minimum.

What is global minima ?

The global minimum in the context of optimization and machine learning refers to the lowest possible value of a given function.

When training machine learning models, the objective is often to minimize a loss function, which measures how well the model’s predictions match the actual data.

The global minimum is the point where this loss function has its absolute lowest value, indicating the best possible performance of the model across the entire dataset.

Activation function is the direct relation on the occurrence of vanishing gradient descent and it occurs frequently when a deep neural network is implemented with sigmoid activation function.

Sigmoid activation function takes in the weighted sum and converts its value between 0 and 1.

Gradient descent is calculated and backpropagation occurs, updating the old weights.

Since the derivative of the sigmoid function is 0.25, the updated weight will be almost the same as the old weight. As a result, the model will take more time to reach the global minimum.

Weight Initialization for Deep Networks

Weight initialization is an important design choice when developing deep learning neural network models.

Key points in Weight initialization are :

1. Weights should be small
2. Weights should not be same
3. Weight should have good variance

What will happen when weights are not small ?

If the initialized weight is too high, the product of the learning rate and the derivative of the sigmoid function with respect to the old weight becomes greater than the old weight. As a result, the new weight will be negative, and the model will not converge toward the global minimum. This phenomenon is also called exploding gradient descent.