Dam101_unitthree

Convolutional Neural Networks

In the vast landscape of artificial intelligence, there exists a cornerstone technology that has reshaped our understanding of image processing and pattern recognition: Just as the human brain processes visual information to understand the world around us, CNNs harness the power of deep learning to analyze and interpret images with remarkable precision and efficiency.

In this introduction, we embark on a journey to unravel the mysteries of CNNs, exploring their origins, fundamental concepts, and transformative impact on diverse fields ranging from computer vision to healthcare.

Let’s dive into the fascinating realm of Convolutional Neural Networks, where pixels transform into insights, and innovation knows no bounds.

Introduction

A Convolutional Neural Network (ConvNet/CNN) is a Deep Learning algorithm that can take in an input image, assign importance (learnable weights and biases) to various aspects/objects in the image, and be able to differentiate one from the other.

The pre-processing required in a ConvNet is much lower as compared to other classification algorithms. While in primitive methods filters are hand-engineered, with enough training, ConvNets have the ability to learn these filters/characteristics

A ConvNet effectively captures spatial relationships in images through filter application. With fewer parameters and weight reusability, it fits image datasets better.

Why Convolutional Neural Networks over feeding images directly to ANN.

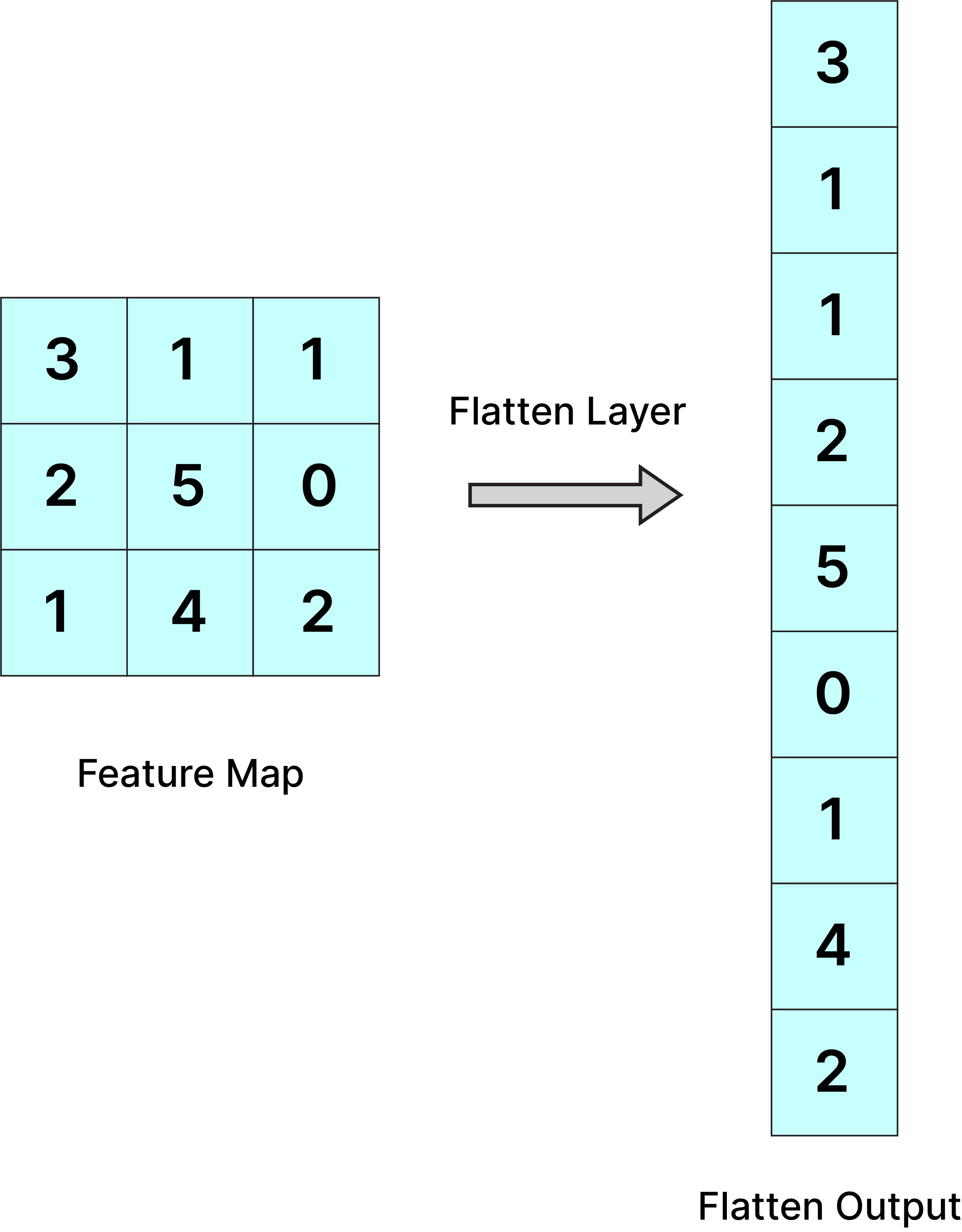
An image is nothing but a matrix of pixel values so why not flatten the matrix into a vector and feed it to ANN like

In the above case the model might be able to draw patterns easily but what of the input image is big (7680×4320), then the model will take computationally heavy resources and latency will also increase therefore Convolutional neural network is implemented to reduce the spatial dimensions of the input image without losing the image important feature.

The role of Convolutional neural network is to reduce the images into a form that is easier to process, without losing features that are critical for getting a good prediction. This is important when we are to design an architecture that is not only good at learning features but also scalable to massive datasets.

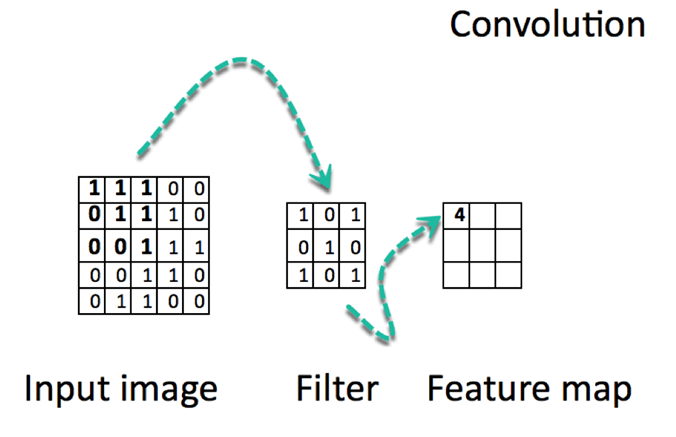
Convolution is a mathematical operation that involves sliding a small matrix (called a kernel or filter) over the input data and computing the element-wise product between the kernel and the overlapped region of the input.

This operation produces a feature map (the end image after convolution )that captures the presence of specific patterns or features in the input data.

CNNs use a series of layers, each of which detects different features of an input image.

What happens at each layer?

A filter of values is slided across the pixel values of an image. When this happens, the values of these pixels are then changed and aggregated based on the matrix multiplication.

What are kernels ?

In Convolutional neural network, the kernel is nothing but a filter that is used to extract the features from the images.

The kernel is a matrix that moves over the input data, performs the dot product with the sub-region of input data, and gets the output as the matrix of dot products.

The output of each layer’s kernels is then passed through a non-linear activation function, such as ReLU, to introduce non-linearity into the network and enable it to learn more complex and abstract features .

Images have properties like edges, shapes, and colors. The combination of these properties generates features. Kernels or filters are responsible for detecting these features in an image.

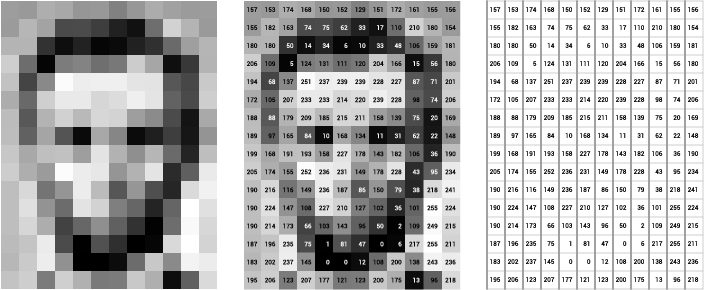
If the image is a grayscale image, then the pixel value will range between 0 and 255 (0 for black and 255 for white).

Grayscale image example.

Example:

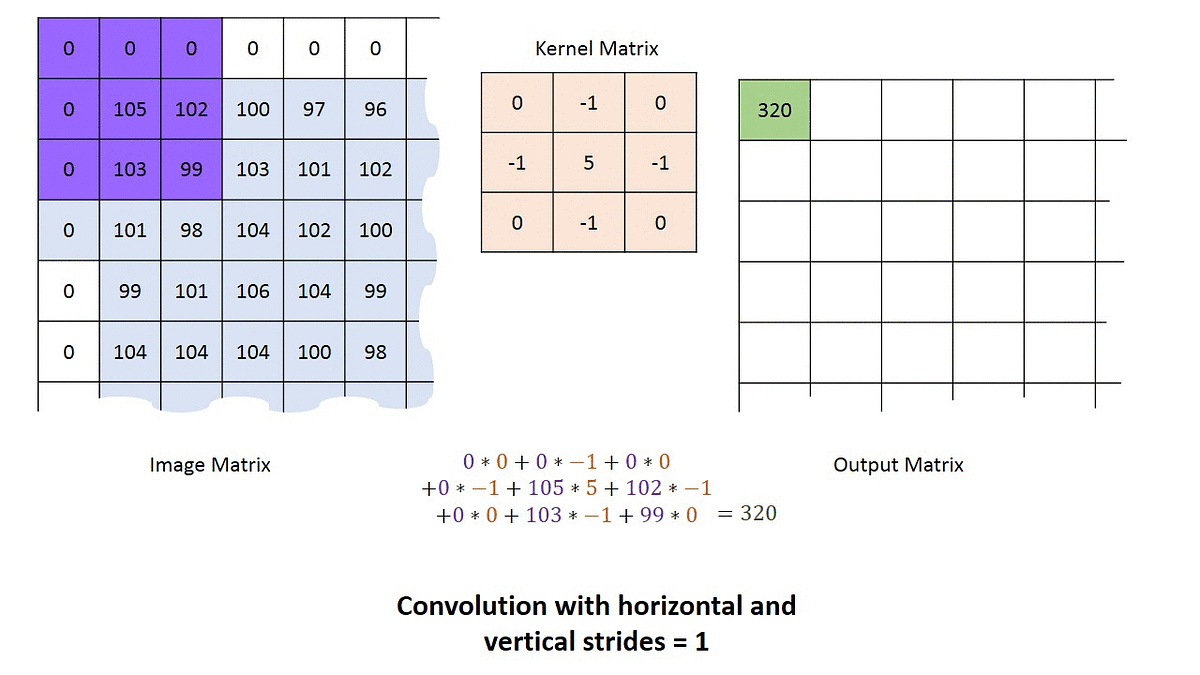
We have an image (5 x 5), a kernel of (3 x 3), and the kernel slides on the image. A new image is generated. The new image generated after the convolution is called the feature map.

When the kernel is placed in a new position, it calculates a dot product. The resulting product is placed in the corresponding position in the feature map.

Any image of size (n x n) when convolved with a kernel (f x f) will generate a feature map of size (n - f + 1) x (n - f + 1).

Convolution acts as a feature detector or edge detector. It detects all the edges in the input image.

Poling

The pooling operation involves sliding a two-dimensional filter over each channel of feature map and summarising the features lying within the region covered by the filter.

A common CNN model architecture is to have a number of convolution and pooling layers stacked one after the other.

Why is Pooling used

• Pooling layer is used to reduce the dimension of the feature map after convolution.

• The pooling layer summarises the features present in a region of the feature map generated by a convolution layer.

• Enhance Feature

Types of pooling

1. Max Pooling
2. Average Pooling

Max Pooling

Max pooling is a pooling operation that selects the maximum element from the region of the feature map covered by the filter.

Thus, the output after max-pooling layer would be a feature map containing the most prominent features of the previous feature map.

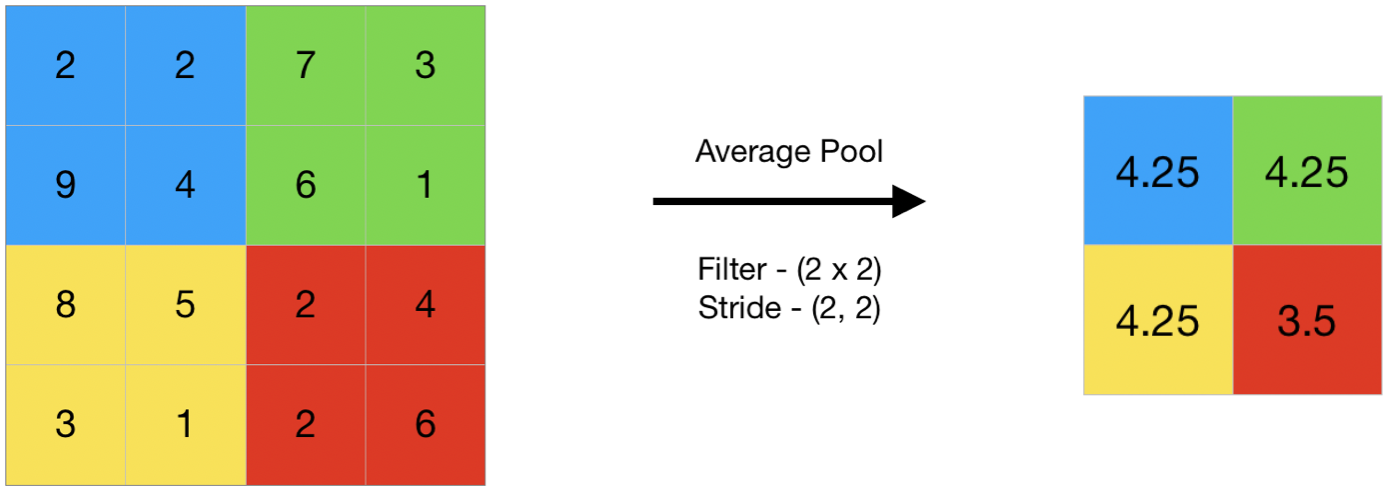
Average Pooling

Average pooling computes the average of the elements present in the region of feature map covered by the filter.

Thus, while max pooling gives the most prominent feature in a particular patch of the feature map, average pooling gives the average of features present in a patch.

Padding

If we simply apply the kernel on the input feature map, then the output feature map will be smaller than the input. This can result in the loss of information at the borders of the input feature map.

In Order to preserve the border information we use padding.

This can be done in two ways:

• Valid Padding: In the valid padding, no padding is added to the input feature map, and the output feature map is smaller than the input feature map. This is useful when we want to reduce the spatial dimensions of the feature maps.

• Same Padding: In the same padding, padding is added to the input feature map such that the size of the output feature map is the same as the input feature map. This is useful when we want to preserve the spatial dimensions of the feature maps.

• The most common padding value is zero-padding, which involves adding zeros to the borders of the input feature map.

  

Padding can help in reducing the loss of information at the borders of the input feature map and can improve the performance of the model.

Problem With Convolution Layers Without Padding

• For a grayscale (n x n) image and (f x f) filter/kernel, the dimensions of the image resulting from a convolution operation is (n – f + 1) x (n – f + 1).

• Also, the pixels on the corners and the edges are used much less than those in the middle.

For Example

• Clearly, pixel A is touched in just one convolution operation and pixel B is touched in 3 convolution operations, while pixel C is touched in 9 convolution operations. In general, pixels in the middle are used more often than pixels on corners and edges. Consequently, the information on the borders of images is not preserved as well as the information in the middle.